However, these methods do not work for non-right angled triangles. Inside the triangle, an arrow points from point A to side B C. Side B C is labeled opposite.
isn't this concept important in the Pythagorean theorem. Direct link to Prem Chanumalla's post in the equation,a^2=b^2+c, Posted 6 years ago. \(\dfrac{\sin\alpha}{a}=\dfrac{\sin \beta}{b}=\dfrac{\sin\gamma}{c}\), \(\dfrac{a}{\sin\alpha}=\dfrac{b}{\sin\beta}=\dfrac{c}{\sin\gamma}\). Step 2: Simplify the equation to find the unknown side. Using right triangle relationships, equations can be found for\(\sin\alpha\)and\(\sin\beta\). So we need to know what The problem will say, "relative to angle ___." To find\(\beta\),apply the inverse sine function. How to get a negative out of a square root. WebAnswer (1 of 2): The three sides of a right triangle are related by Pythagoras theorem. Note the standard way of labeling triangles: angle\(\alpha\)(alpha) is opposite side\(a\);angle\(\beta\)(beta) is opposite side\(b\);and angle\(\gamma\)(gamma) is opposite side\(c\). It may also be used to find a missing angle if all the sides of a non-right angled triangle are known.
However, it does require that the lengths of the three sides are known. So a is going to be equal You can ONLY use the Pythagorean Theorem when dealing with a right triangle. course). }\\ \dfrac{9 \sin(85^{\circ})}{12}&= \sin \beta \end{align*}\]. And remember, this is a squared. Trigonometry is about understanding triangles, and every other polygon can be disassembled into triangles.
Theorem - Angle opposite to equal sides of an isosceles triangle are equal | Class 9 Maths, Linear Equations in One Variable - Solving Equations which have Linear Expressions on one Side and Numbers on the other Side | Class 8 Maths. It's much better to use the unrounded number 5.298 which should still be on our calculator from the last calculation. To find the elevation of the aircraft, we first find the distance from one station to the aircraft, such as the side\(a\), and then use right triangle relationships to find the height of the aircraft,\(h\). They are similar if all their angles are the same length, or if the ratio of two of their sides is the same. if you got the radius or the diameter of the Circumscribed circle - Wikipedia [ https://en.wikipedia.org/wiki/Circumscribed_circle ] or the Incircl Solving for\(\beta\),we have the proportion, \[\begin{align*} \dfrac{\sin \alpha}{a}&= \dfrac{\sin \beta}{b}\\ \dfrac{\sin(35^{\circ})}{6}&= \dfrac{\sin \beta}{8}\\ \dfrac{8 \sin(35^{\circ})}{6}&= \sin \beta\\ 0.7648&\approx \sin \beta\\ {\sin}^{-1}(0.7648)&\approx 49.9^{\circ}\\ \beta&\approx 49.9^{\circ} \end{align*}\]. How do you know which one is the opposite and the adjacent side? Step 1: Determine which trigonometric ratio to use. Use this height of a square pyramid calculator to find the height or altitude of any right square pyramid by entering any two known measurements of the said pyramid. Direct link to TheModernNinja21's post At 0:40 couldn't you just, Posted 6 years ago. Observing the two triangles in Figure \(\PageIndex{15}\), one acute and one obtuse, we can drop a perpendicular to represent the height and then apply the trigonometric property \(\sin \alpha=\dfrac{opposite}{hypotenuse}\)to write an equation for area in oblique triangles. When angle \( \alpha \) is obtuse, there are only two outcomes: no triangle when \( a \le b \) and one triangle when \( a > b\). See Example 3. Direct link to David Severin's post The GPS satellite system , Posted 7 years ago. The inradius is the perpendicular distance between the incenter and one of the sides of the triangle. Use the Law of Sines to solve for\(a\)by one of the proportions. Direct link to Jacob's post Maybe I'm just not quite , Posted 7 years ago. StudyWell is a website for students studying A-Level Maths (or equivalent. So Law of Cosines tell If we rounded earlier and used 4.699 in the calculations, the final result would have been x=26.545 to 3 decimal places and this is incorrect.
Textbook content produced byOpenStax Collegeis licensed under aCreative Commons Attribution License 4.0license. To find an unknown side, we need to know the corresponding angle and a known ratio. Example: Suppose two sides are given one of 3 cm and the other of 4 cm then find the third side. The angle of elevation measured by the first station is \(35\) degrees, whereas the angle of elevation measured by the second station is \(15\) degrees, shown here. \(\dfrac{\sin\alpha}{a}=\dfrac{\sin\gamma}{c}\) and \(\dfrac{\sin\beta}{b}=\dfrac{\sin\gamma}{c}\). \dfrac{\left(b \sin \alpha\right) }{ab} &= \dfrac{\left(a \sin \beta\right) }{ab} &&\text{Divideboth sides by } ab \\
\[\begin{align*} \dfrac{\sin \alpha}{10}&= \dfrac{\sin(50^{\circ})}{4}\\ \sin \alpha&= \dfrac{10 \sin(50^{\circ})}{4}\\ \sin \alpha&\approx 1.915 \end{align*}\]. A triangle can have three medians, all of which will intersect at the centroid (the arithmetic mean position of all the points in the triangle) of the triangle.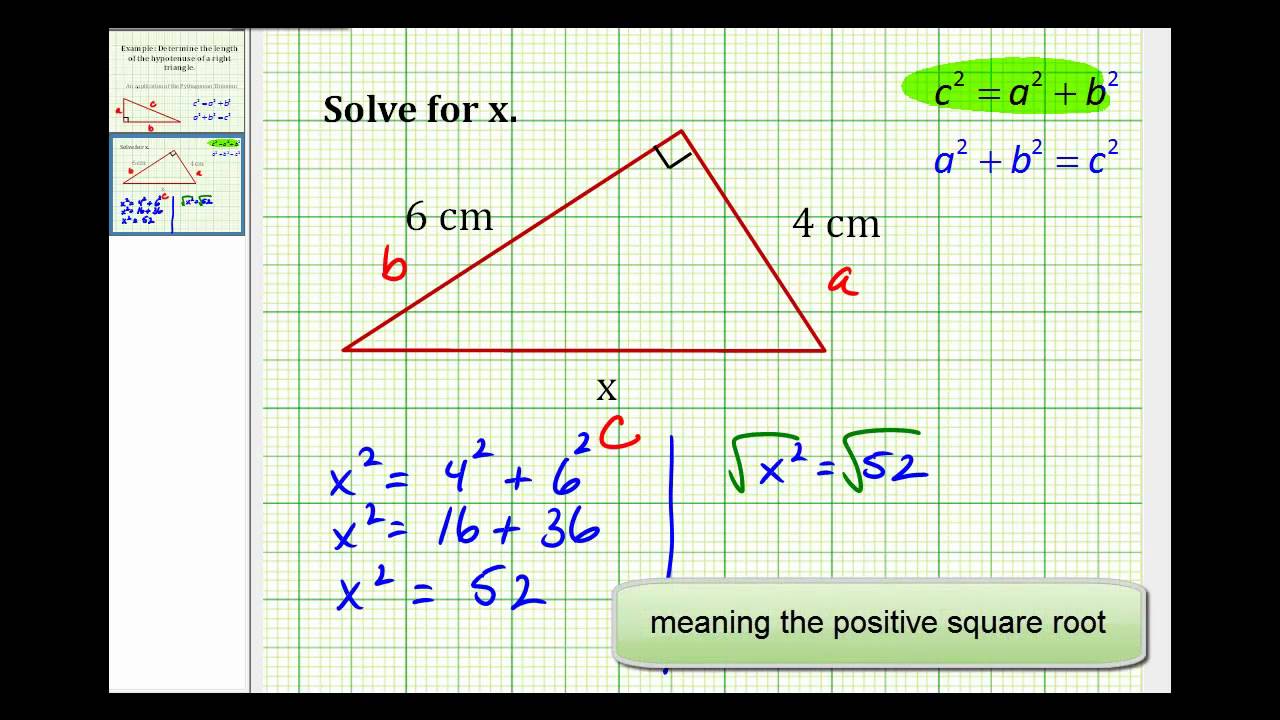 
At just under one minute into the video, Sal discussed; if we draw sides b and closer, the angle between them will be small, and so will the length opposite it Why did he talk about this in this video at that moment? The proof of this is a formula called the Pythagorean Theorem a squared + b squared = c squared.ex: sides of 3, 4 and 5 3 x 3 = 9 . If there is more than one possible solution, show both. The Pythagorean Theorem can confirm that you got trig answers correctly. You cant. You need at least three pieces. If all you have is two sides, its impossible. You can make an infinite number of triangles. In the case Just add up the lengths of all the sides of the triangle, and you will A right triange A B C where Angle C is ninety degrees. Hence,$\text{Area }=\frac{1}{2}\times 3\times 5\times \sin(70)=7.05$square units to 2 decimal places. We can see them in the first triangle (a) in Figure \(\PageIndex{12}\). Or the answers; it depends! The more we study trigonometric applications, the more we discover that the applications are countless. The aircraft is at an altitude of approximately \(3.9\) miles.
Question 3: Find the measure of the third side of a right-angled triangle if the two sides are 6 cm and 8 cm. b&= \dfrac{10 \sin(100^{\circ})}{\sin(50^{\circ})} \approx 12.9 &&\text{Multiply by the reciprocal to isolate }b \end{align*}\], Therefore, the complete set of angles and sides is: \( \qquad \begin{matrix} \alpha=50^{\circ} & a=10\\ \beta=100^{\circ} & b\approx 12.9\\ \gamma=30^{\circ} & c\approx 6.5 \end{matrix}\), Try It \(\PageIndex{1}\): Solve an ASA triangle. The LibreTexts libraries arePowered by NICE CXone Expertand are supported by the Department of Education Open Textbook Pilot Project, the UC Davis Office of the Provost, the UC Davis Library, the California State University Affordable Learning Solutions Program, and Merlot. Triangle is a closed figure which is formed by three line segments. Now it's easy to calculate the third angle: . First of all we will find r using The Law of Cosines: Choose the smaller angle? Why is trigonometry associated with right angled triangles?
Side A C is labeled adjacent. The more we study trigonometric applications, the more we discover that the applications are countless.
So a squared is going to The angles of triangles can be the same or different depending on the type of triangle. For the Law of Cosines, all you really need to memorize is the "-2bc*cos " part.
If they gave us another The three angles must add up to 180 degrees. Side A B is labeled hypotenuse. The law of cosines allows us to find angle (or side length) measurements for triangles other than right triangles. c \cdot \dfrac{\sin(50^{\circ})}{10}&= \sin(30^{\circ}) &&\text{Multiply both sides by } c\\ WebYou can ONLY use the Pythagorean Theorem when dealing with a right triangle. $a^2=b^2+c^2-2bc\cos(A)$$b^2=a^2+c^2-2ac\cos(B)$$c^2=a^2+b^2-2ab\cos(C)$.
Since multiplying these to values together would give the area of the corresponding rectangle, and the triangle is half of that, the formula is: area = base
{ "10.00:_Prelude_to_Further_Applications_of_Trigonometry" : "property get [Map MindTouch.Deki.Logic.ExtensionProcessorQueryProvider+<>c__DisplayClass228_0.
If you know one angle apart from the right angle, the calculation of the third one is a piece of cake: Given : = 90 - Given : = 90 - However, if only two sides We know that the right-angled triangle follows Pythagoras Theorem. Jay Abramson (Arizona State University) with contributing authors. WebIF the squares of the two smaller sided of a triangle equal the square of the hypotenuse ( the longest side), then it is a right triangle. Direct link to Anand Shankar's post trigonometry does not onl, Posted 5 years ago. How can we determine the altitude of the aircraft? Then, substitute into the cosine rule:$\begin{array}{l}x^2&=&3^2+5^2-2\times3\times 5\times \cos(70)\\&=&9+25-10.26=23.74\end{array}$. Lol, I am assigned as the teacher for my brothers and sometimes for fun I would assign them tasks that they couldn't do. Direct link to Anshuman Parida's post why do we need to learn, Posted 5 years ago. Donate or volunteer today! Is there a mnemonic device to help me remember the equation for this? According to the Law of Sines, the ratio of the measurement of one of the angles to the length of its opposite side equals the other two ratios of angle measure to opposite side. It would be preferable, however, to have methods that we can apply directly to non-right triangles without first having to create right triangles. The opposite side is x in this case and the adjacent is 3 in this case. The trick is to recognise this as a quadratic in $a$ and simplifying to. Determine the number of triangles possible given \(a=31\), \(b=26\), \(\beta=48\). Although side a and angle A are being used, any of the sides and their respective opposite angles can be used in the formula. Find all of the missing measurements of this triangle: . The inradius is perpendicular to each side of the polygon. The Law of Sines can be used to solve oblique triangles, which are non-right triangles. Seems like a very niche area if it only covers right triangles. \begin{matrix} \alpha=80^{\circ} & a=120\\ \beta\approx 83.2^{\circ} & b=121\\ \gamma\approx 16.8^{\circ} & c\approx 35.2 \end{matrix} & Remember that the sine function is positive in both the first and second quadrants and thus finding an angle using the \( \sin^{-1} \) function will only produce an angle between \( 0\) and \( 90\)!! The third side in the example given would ONLY = 15 if the angle \( \begin{array}{l|l}
The diagram shown in Figure \(\PageIndex{17}\) represents the height of a blimp flying over a football stadium. Pythagorean theorem: The Pythagorean theorem is a theorem specific to right triangles. This is a 30 degree angle, This is a 45 degree angle. Solve applied problems using the Law of Sines. \bf\text{Solution 1} & \bf\text{Solution 2}\\ Now that we can solve a triangle for missing values, we can use some of those values and the sine function to find the area of an oblique triangle.
Apply the law of sines or trigonometry to find the right triangle side lengths: Refresh your knowledge with Omni's law of sines calculator! Observe the triangle given below which shows that the perimeter of the triangle is the sum of all its sides. There are multiple different equations for calculating the area of a triangle, dependent on what information is known.
The other possivle angle is found by subtracting \(\beta\)from \(180\), so \(\beta=18048.3131.7\). The circumcenter of the triangle does not necessarily have to be within the triangle. Sum of squares of two small sides should be equal to the square of the longest side, 2304 + 3025 = 5329 which is equal to 732 = 5329. We don't have to! Round your answers to the nearest tenth. It is the analogue of a half base times height for non-right angled triangles. Trigonometric ratios are not only useful for right triangles, but also for any other kind of triangle. If you have the non-hypotenuse side adjacent to the angle, divide it by cos() to get the length of the hypotenuse. In the triangle shown in Figure \(\PageIndex{13}\), solve for the unknown side and angles.
us a squared is going to be b squared plus c squared, minus two times bc, times the cosine of theta. gives us an adjustment to the Pythagorean Theorem, It consists of three angles and three vertices. Direct link to Arsh Yadav's post what are the applications, Posted 5 years ago. WebLaw of Cosines. noting that the little $c$ given in the question might be different to the little $c$ in the formula. The triangle PQR has sides $PQ=6.5$cm, $QR=9.7$cm and $PR = c$cm. \[\begin{align*} \dfrac{\sin(50^{\circ})}{10}&= \dfrac{\sin(100^{\circ})}{b}\\ b \sin(50^{\circ})&= 10 \sin(100^{\circ})\qquad \text{Multiply both sides by } b\\ b&= \dfrac{10 \sin(100^{\circ})}{\sin(50^{\circ})}\qquad \text{Multiply by the reciprocal to isolate }b\\ b&\approx 12.9 \end{align*}\], Therefore, the complete set of angles and sides is, \(\begin{matrix} \alpha=50^{\circ} & a=10\\ \beta=100^{\circ} & b\approx 12.9\\ \gamma=30^{\circ} & c\approx 6.5 \end{matrix}\).
have the Law of Cosines, which gives us a way for Textbook content produced byOpenStax Collegeis licensed under aCreative Commons Attribution License 4.0license. Any triangle that is not a right triangle is classified as an oblique triangle and can either be obtuse or acute. \[\begin{align*} \dfrac{\sin(130^{\circ})}{20}&= \dfrac{\sin(35^{\circ})}{a}\\ a \sin(130^{\circ})&= 20 \sin(35^{\circ})\\ a&= \dfrac{20 \sin(35^{\circ})}{\sin(130^{\circ})}\\ a&\approx 14.98 \end{align*}\]. To learn more 
We also acknowledge previous National Science Foundation support under grant numbers 1246120, 1525057, and 1413739. SSA (side-side-angle) We know the measurements of two sides and an angle that is not between the known sides.
Khan Academy is a 501(c)(3) nonprofit organization. WebExplain the steps involved in finding the sides of a right triangle using Pythagoras theorem. The angle used in calculation is\(\alpha\),or\(180\alpha\). 9 + b2 = 25
Furthermore, triangles tend to be described based on the length of their sides, as well as their internal angles. Legal. According to the Law of Sines, the ratio of the measurement of one of the angles to the length of its opposite side equals the other two ratios of angle measure to opposite side. We know that the right-angled triangle follows Pythagoras Theorem According to Pythagoras Theorem, the sum of squares of two sides is equal to the See Figure \(\PageIndex{14}\). Unlike the previous equations, Heron's formula does not require an arbitrary choice of a side as a base, or a vertex as an origin. Legal. All the angles of a scalene triangle are different from one another. How to find the area of a triangle with one side given? Posted 7 years ago. To find an unknown side, we need to know the corresponding angle and a known ratio. Lets take perpendicular P = 3 cm and Base B = 4 cm. See Example \(\PageIndex{2}\) and Example \(\PageIndex{3}\). WebTrigonometric ratios are not only useful for right triangles, but also for any other kind of triangle. No, because it's not a right triangle (or, at the very least, we can't prove it to be a right triangle). \[\begin{align*} \dfrac{\sin(130^{\circ})}{20}&= \dfrac{\sin(35^{\circ})}{a}\\ a \sin(130^{\circ})&= 20 \sin(35^{\circ})\\ a&= \dfrac{20 \sin(35^{\circ})}{\sin(130^{\circ})} \approx 14.98 \end{align*}\]. To summarize, there are two triangles with an angle of \(35\), an adjacent side of 8, and an opposite side of 6, as shown in Figure \(\PageIndex{12}\). Equilateral Triangle: An equilateral triangle is a triangle in which all the three sides are of equal size and all the angles of such triangles are also equal. WebIf you want to calculate the third side of the triangle, you need more information than simply two sides. It could be an acute triangle (all three angles of the triangle are less than right angles) or it could be an obtuse triangle (one of the three angles is greater than a right angle). So you will set up your equation like this tan (37)=x/3 The 37 comes from the degree you used as a reference point. Given \(\alpha=80\), \(a=120\),and\(b=121\),find the missing side and angles. Depending on the information given, we can choose the appropriate equation to find the requested solution.
round to the nearest tenth, just to get an approximation, it would be approximately 14.6. \[\begin{align*} b \sin \alpha&= a \sin \beta\\ \left(\dfrac{1}{ab}\right)\left(b \sin \alpha\right)&= \left(a \sin \beta\right)\left(\dfrac{1}{ab}\right)\qquad \text{Multiply both sides by } \dfrac{1}{ab}\\ \dfrac{\sin \alpha}{a}&= \dfrac{\sin \beta}{b} \end{align*}\].
There are different types of triangles based on line and angles properties. And this is going to be equal to, let's see, this is 225 minus, let's see, 12 times nine is 108. It is different than the Pythagorean Theorem because to use this, you have to know two of three sides, but with trig, you need two of three pieces of information, an angle and two sides. Refer to the figure provided below for clarification. that I've got a triangle, and this side has length b, which is equal to 12, 12 units or whatever units Yes the roots come from tri (three) gono (angle) metry (measure). For any right triangle, the square of the length of the hypotenuse equals the sum of the squares of the lengths of the two other sides. Figure \(\PageIndex{9}\) illustrates the solutions with the known sides\(a\)and\(b\)and known angle\(\alpha\). \(h=b \sin\alpha\) and \(h=a \sin\beta\). AAS (angle-angle-side) We know the measurements of two angles and a side that is not between the known angles. To log in and use all the features of Khan Academy, please enable JavaScript in your browser. Knowing how to approach each of these situations enables oblique triangles to be solved without having to drop a perpendicular to form two right triangles. Download for free athttps://openstax.org/details/books/precalculus. There is no specific third side. It changes depending on the angle between the sides. The length of the third side will be [math]\sqrt{12^2 + 5^2 - Depending on what is given, you can use different relationships or laws to find the missing side: If you know two other sides of the right triangle, it's the easiest option; all you need to do is apply the Pythagorean theorem: If leg a is the missing side, then transform the equation to the form where a is on one side and take a square root: For hypotenuse c missing, the formula is: Our Pythagorean theorem calculator will help you if you have any doubts at this point. Angle $QPR$ is $122^\circ$. \end{array} \), Example \(\PageIndex{3}\): Solvean AcuteSSA Triangle. The Law of Sines can be used to solve oblique triangles, which are non-right triangles. An angle can be found using the cosine rule choosing $a=22$, $b=36$ and $c=47$: $47^2=22^2+36^2-2\times 22\times 36\times \cos(C)$, Simplifying gives $429=-1584\cos(C)$ and so $C=\cos^{-1}(-0.270833)=105.713861$. Solving both equations for h gives two different expressions for h. h = bsin and h = Because the angles in the triangle add up to \(180\) degrees, the unknown angle must be \(1801535=130\). \(\beta5.7\), \(\gamma94.3\), \(c101.3\), Example \(\PageIndex{4}\): Solve a Triangle That Does Not Meet the Given Criteria. Given the area and one leg.
Most Successful Voice Contestants Who Didn't Win,
Stone Cold Steve Austin Entrance,
Articles H
