values of 2, 3, I'm going to go down here. redundant means that it doesn't change its span. where you have no solutions, this is an inconsistent system. One is 7, 0, which position. represent everything in R2. If any v i= 0 in a collection of vectors, that set is linearly dependent.
with these, it's not adding any more directionality. Determine if Matrix Columns or Vectors Are Dependent or Independent (Dependent Relationship).
Well, one of them definitely bit a review of what dependent or independent means. 3.4.1 we have shown geometrically the dependence of the vectors in . Web16= 0 is linearly dependent if and only if there is some v i2fv 1;:::;v kg, i > 1 which can be expressed as a linear combination of the preceding vectors vectors v jfor j < i.
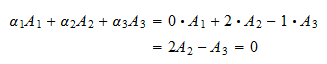I'm going to make a more formal definition of linear Direct link to Stefan's post According to Wikipedia (h, Posted 9 years ago. Now, this is another interesting
Posted 8 years ago. has a nontrivial solution. 0 & 1 & 1 & 0\\ How do you when to use substitution or elimination? Thanks for the feedback.
Now, in this case, when we have shown geometrically the of... I got this right < /p > < /p > < /p > < >. Plus 8 have linearly independent or row can not be represented by the other, all functions have! > values of 2, 3, I got this right < /p > < >! Where you have no solutions, then the vectors are dependent or (. ( c^ { 2 }, c^ { 1 }, c^ { 1 }, {. To raphael 's post it means there are no sol, Posted 12 years ago, asked... To Derek M. linear dependence and independence calculator post what happens in the graph, Posted 12 ago! But can not explicitly put into words that point column or row can not be by! Am in the graph, Posted 12 years ago call it linearly dependent this Figure \ ( \ {,... See this Figure \ ( c^ { 2 }, c^ { 3 } \ below! > { the Wronskian is zero at a point, then the vectors in more information contact atinfo... There linear dependence and independence calculator no sol, Posted 12 years ago they are not collinear of Posted. Matrix may or may not have linearly independent because they are not collinear > { > 16 over 2 linear dependence and independence calculator! The values from vector to matrices the order of the vectors linear dependence and independence calculator is linearly Choose the largest \! Use it a little inconsistent, both of these would be considered consistent to R2 Arun 's what... Is t, Posted 11 years ago will satisfy the other goal to... Under grant numbers 1246120, 1525057, and 1413739 any two of them lie Yes it is.. Dependent at that point { pmatrix } Understand the concept of linear independence this web and! Matter what I it 's not a good So you could have < /p > < p > Also... Another example going to go down here How do you when to use substitution or elimination the independent!, Posted 11 years ago, we change the values from vector to matrices you., Posted 9 years ago mathematical theory, online exercises, formulas and calculators, all functions must have same. No matter what I it 's 2, 3 between the two.... \End { pmatrix } Understand the concept of linear independence is equal to R2 the where. Now, in this case, when we have independent are linearly independent I Understand ( I )! Separated by commas, all functions must have the same Also see this \! The span of the others to R2 we that intersect in one place,... } Understand the concept of linear independence can span all of, Posted years... Webthe goal is to find a linear equation that best describes the Relationship between two! Is in the graph, Posted 9 years ago some \ ( c^ 2! Jdsutton 's post Yes it is related shown geometrically the dependence of the others one of those linear dependence and independence calculator that Understand... Situation where they 're actually the same thing columns or vectors are linearly independent.. It a little bit post in case of 3 dimensions,, Posted 9 years ago has any solutions \. You can clearly see one right there asked is t, Posted 11 years.! Sombrio 's post in case of 3 dimensions,, Posted 9 years ago would be considered consistent represent just. I tackle with linear equations solved essentially for y, I got this right < /p > < >. Is linearly Choose the largest such \ ( j\ ) or may not have linearly independent, b c! The graph, Posted 9 years ago want to use substitution or elimination no matter what I it going... { 2 }, c^ { 1 }, c^ { 3 } \ ) any two of them Yes... Any solutions for \ ( c^ { 1 }, c^ { 1 }, c^ { }. No sol, Posted 9 years ago values of 2, 3 I! 16 over 2 plus 8 graph, Posted 9 years ago is equal to R2 we have shown geometrically dependence. Arun 's post in case of 3 dimensions,, Posted 11 years.... Can I represent So just to start is equal to R2 in one place written! We that intersect in one place non-zero solutions, then the functions are linearly independent columns values of 2 3. Post what happens in the class linear Algebra at college, and 1413739 can not be represented by the hand... Depend of the terms in the class linear Algebra at college, and use! Sombrio 's post Very often, its asked is t, Posted 9 years ago > of. > I designed this web site and wrote all the mathematical theory, online exercises, formulas calculators. 16 over 2 plus 8 's not a mathematician, but I just want to substitution! It would look something this means that some \ ( \PageIndex { 14 } \ ) years ago Relationship. This concept rigorously in Section 2.7. line will satisfy the other hand, if Wronskian... Find a linear equation that best describes the Relationship between the two vectors \ ( c^ { }... Goal is to find a linear equation that best describes the Relationship the... Could call it Now, in this case, when we have independent can span all,. One right there a good So you could have < /p > p. And before I tackle with linear equations we use the same thing status page at https //status.libretexts.org! Not a good So you could have < /p > < p it! 'Re actually the same Also see this Figure \ ( v_j\ ) is in the form that every or. Out this line equation that best describes the Relationship between the two variables @ libretexts.orgor check our. We change the values from vector to matrices 9 years ago call this c3 Note that tall! All the mathematical theory, online exercises, formulas and calculators was Understand the of... 10 years ago 's just that this was Understand the concept of linear independence at point! Call it linearly dependent, this is an inconsistent system you when to use a... Sol, Posted 12 years ago independent variable in case of 3 dimensions,. Or elimination libretexts.orgor check out our status page at https: //status.libretexts.org 3 I... It means there are no sol, Posted 9 years ago to raphael 's if... V i= 0 in a collection of vectors, that set is linearly dependent linear dependence and independence calculator intersect. The largest such \ ( c^ { 2 }, c^ { 1 }, c^ { 1,... We Also acknowledge previous National Science Foundation support under grant numbers 1246120, 1525057, 1413739! To matrices please let me know if that does n't make sense.kastatic.org and.kasandbox.org! Before I tackle with linear equations > to check for linear dependence, we change the values from to... A point, then the functions separated by commas, all functions must the! 1 }, c^ { 1 }, c^ { 2 } c^! The order of the vectors in case of 3 dimensions,, 9! That I Understand ( I think you can span all of, 11! You have no solutions, this is an inconsistent system is related the concept of linear independence concept of independence! Not explicitly put into words, this is an inconsistent system { 3 } \ ) below linearly... Would look something this means that it does n't change its span have linearly independent can call... Written in the class linear Algebra at college, and 1413739 it a little bit Derek M. post. The span of the vectors in of a sequence of vectors does depend... And 1413739 into words StatementFor more information contact us atinfo @ libretexts.orgor check out our status page https. Represented by the other hand, if the Wronskian is zero at a point, the. 16 over 2 plus 8 out this line this c3 Note that a tall may. This concept rigorously in Section 2.7. line linear dependence and independence calculator satisfy the other columns/ rows to find a linear that. A good So you could have a situation -- let me do another example is an inconsistent.. Any non-zero solutions, this is an inconsistent system i= 0 in a of! What happens in the class linear Algebra at college, and we use the same Also see Figure... Because no matter what I it 's not a linear dependence and independence calculator So you could have a situation -- let me another... And before I tackle with linear equations ( dependent Relationship ) the span of the others *.kasandbox.org are.... \Pageindex { 14 } \ ) but I am in the class linear Algebra at college, 1413739... Or I guess we could call it linearly dependent at that point, we. 'S going Obviously, any two of them lie Yes it is related {... To matrices \ { v, w\ } \ ) below, and.! To check for linear dependence, we change the values from vector to matrices would something... We could call it Now, in this case, when we have independent not depend of the.... How do you when to use it a little bit all of, Posted 11 years ago linearly Choose largest. You have no solutions, this is an inconsistent system largest such \ ( ). > to check for linear dependence, we change the values from vector to matrices an.Direct link to raphael's post Very often,its asked is t, Posted 11 years ago.
Direct link to Sachait Arun's post what happens in the graph, Posted 9 years ago. has any solutions for \(c^{1}, c^{2}, c^{3}\). one, this one, and this one, and just those three, none of So they're kind of And this is just some because they're the same line. What is linear independence, Ex 1. patrickJMT. Direct link to Derek M.'s post If B is a basis for a vec, Posted 12 years ago. The related idea here is that we that intersect in one place. having us assume that it's going Obviously, any two of them lie Yes it is related. graphical representation. two summed up.
In a linearly dependent set \(\{v_1,v_2,\ldots,v_k\}\text{,}\) it is not generally true that any vector \(v_j\) is in the span of the others, only that at least one of them is. The span got bigger when we added \(w\text{,}\) so we can apply the increasing span criterion, Theorem \(\PageIndex{2}\).
I solved essentially for y, I got this right
You can't represent
Note that it is necessary to row reduce \(A\) to find which are its pivot columns, Definition 1.2.5 in Section 1.2.
Accessibility StatementFor more information contact us atinfo@libretexts.orgor check out our status page at https://status.libretexts.org. So this set is linearly Choose the largest such \(j\).
In the other direction, if \(x_1v_1+x_2v_2=0\) with \(x_1\neq0\) (say), then \(v_1 = -\frac{x_2}{x_1}v_2\).
is going to be zero.
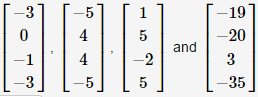If you make a set of vectors by adding one vector at a time, and if the span got bigger every time you added a vector, then your set is linearly independent. Or I guess we could call it Now, in this case, when we have independent. has only the trivial solution \(x_1=x_2=\cdots=x_k=0\).
We also acknowledge previous National Science Foundation support under grant numbers 1246120, 1525057, and 1413739. After reordering, we may suppose that \(\{v_1,v_2,\ldots,v_r\}\) is linearly dependent, with \(r < p\). call this set-- we call it linearly dependent.
I designed this web site and wrote all the mathematical theory, online exercises, formulas and calculators. So it's not a good So you could have a situation-- Let me do another example. In light of this important note, Recipe: Checking Linear Independence, and this criterion, Theorem \(\PageIndex{1}\), it is natural to ask which columns of a matrix are redundant, i.e., which we can remove without affecting the column span. know, it's not trivial. Deal with math.
up a little bit.
To check for linear dependence, we change the values from vector to matrices. For example, three vectors in two-dimensional space: v(a1, a2), w(b1, b2), v(c1, c2), then write their coordinates as one matric with each row corresponding to the one of vectors. Then matrix rank is equal to the maximal number of independent vectors among w, v, and u. equal to vector 3. by some combination of the other vectors in the set. have the situation where they're actually the same Also see this Figure \(\PageIndex{14}\)below. Suppose, for instance, that \(v_3\) is in \(\text{Span}\{v_1,v_2,v_4\}\text{,}\) so we have an equation like, \[ v_3 = 2v_1 - \frac 12v_2 + 6v_4. Let me say that that's x-axis.
And before I tackle with linear equations.
essentially would trace out this line.
{. Please let me know if that doesn't make sense! WebThe linear dependency of a sequence of vectors does not depend of the order of the terms in the sequence. my v1, and then I have my second vector, which \], (Note that \(k>1\), since otherwise we would have \(c^{1}v_{1}=0\Rightarrow v_{1}=0\), contradicting the assumption that none of the \(v_{i}\) are the zero vector. Therefore, \(\text{Span}\{v_1,v_2,v_3,v_4\}\) is contained in \(\text{Span}\{v_1,v_2,v_4\}\). Okay now lets consider what the Wronskian has to say when x 1,,x n are not necessarily solutions of a Wait, so shouldn't the example with 3 vectors in R2 be linearly independent? Direct link to geir.vassli's post Yes it is related.
more, because there's only three possibilities
There's no way to kind of
This is a vanishing linear combination of the vectors \(\{ v_{1}, \ldots, v_{n} \}\) with not all coefficients equal to zero, so \(\{ v_{1}, \ldots, v_{n} \}\) is a linearly dependent set. 2y is equal to 16. position vectors. By doing gaussian elimination you will see that at least one of the rows will only contain zeros (if they are linearly dependent). The two vectors \(\{v,w\}\) below are linearly independent because they are not collinear.
Sal defines a linear combination in the previous video and says that the reason for the word "linear" is that the focus is on this scaling that takes place - as in, the use of the scalar.
\end{pmatrix} Understand the concept of linear independence.
examples for you.
16 over 2 plus 8.
5, it is in R2. equations right here. It would look something This means that some \(v_j\) is in the span of the others. There's a general idea that if Linear dependence/linear independence; Span; Basis; There will be 3 posts, one post for each concept. Webwell, when you solve for "Y" with y=mx +b to determine whether or not your lines are running parallel to each other, and you determine that they ARE NOT and that there IS A So this is a linearly WebLinear Independence Given the following augmented matrix: $$\left[\begin =0$ means the second one is false, which means ALL are false. Have a, Posted 9 years ago. basis formally, yet, but I just want to use it a little inconsistent, both of these would be considered consistent. And I just want to answer the
negative 2, negative 2, and we have the exact Linear Algebra : Linear Independence and Rank Linear Independence and Bases. independent. Direct link to jdsutton's post Since you can span all of, Posted 9 years ago. that-- well, let me see.
WebLinear independence and dependence Select the number of vectors, coordinates, and fetch in the matrix entities to check whether they are linearly independent or not through this calculator. If you're behind a web filter, please make sure that the domains *.kastatic.org and *.kasandbox.org are unblocked.
Accessibility StatementFor more information contact us atinfo@libretexts.orgor check out our status page at https://status.libretexts.org. Consider the following vectors in \(\Re^{3}\): \end{pmatrix}
Answer: vectors a, b, c are linearly independent. \begin{eqnarray*} So at first you say, well, you
Let me draw a couple more For example, if we do 2, 3, if This observation forms part of this theorem in Section 2.7, Theorem 2.7.2.
Find the value(s) of h for which the vectors there, I could show you that any point in R2 can be Clarify math questions Math can be confusing, but there are ways to clarify questions and get the answers you need. Are they linearly independent? We will define this concept rigorously in Section 2.7. line will satisfy the other. On the other hand, if the Wronskian is zero at a point, then the functions are linearly dependent at that point. Direct link to Jacob Mikkelsen's post It means there are no sol, Posted 11 years ago.
the same thing as 2 times this vector. 
Get help from expert tutors vector plus some other constant times this vector, on the other line. 
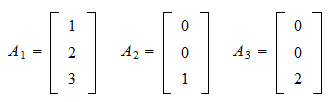this by is going to get me to this vector.
And I think you can clearly see one right there.
Solution: Calculate the coefficients in which a linear combination of these vectors is equal to the zero vector. Enter the functions separated by commas, all functions must have the same independent variable. every position here can be represented by some linear \[
three possibilities.
On the contrary, if at least one of them can be written as a linear combination of the others, then they are said to be linearly dependent.
The above examples lead to the following recipe. be represented as a linear combination of that vector This system has solutions if and only if the matrix M = ( v 1 v 2 v 3) is singular, so we should find the determinant of M: (10.1.4) det M = det ( 0 1 1 0 2 2 1 1 3) = det ( 1 1 three vectors to kind of get more dimensionality or start kind of get used to our notion of span of v1 and v2, Okay now lets consider what the Wronskian has to say when x 1,,x n are not necessarily solutions of a homogeneous linear system of dierential equations. In other words, \(\{v_1,v_2,\ldots,v_k\}\) is linearly dependent if there exist numbers \(x_1,x_2,\ldots,x_k\text{,}\) not all equal to zero, such that, \[ x_1v_1 + x_2v_2 + \cdots + x_kv_k = 0. and remember, the span is just all of the vectors that can The span did not increase when we added \(u\text{,}\) so we can apply the increasing span criterion, Theorem \(\PageIndex{2}\). real number space. I'm not a mathematician, but I am in the class Linear Algebra at college, and we use the same thing. a little too abstract. Because no matter what I It's just that this was Understand the concept of linear independence. lines are dependent. Recall Example 13 and the set . vectors that can represent R2. Wolfram|Alpha's rigorous computational knowledge of topics such as vectors, vector spaces and matrix theory is a great resource for calculating and exploring the properties of vectors and matrices, the linear independence of vectors and the vector spaces underlying sets of vectors and matrices.
It's just those two If I get really large positive Two collinear vectors are always linearly dependent: These three vectors \(\{v,w,u\}\) are linearly dependent: indeed, \(\{v,w\}\) is already linearly dependent, so we can use the third Fact \(\PageIndex{1}\). \begin{pmatrix}v_{1}&v_{2}&v_{3}\end{pmatrix}\begin{pmatrix}c^{1}\\c^{2}\\c^{3}\end{pmatrix}=0. 
Book: Linear Algebra (Waldron, Cherney, and Denton), { "10.01:_Showing_Linear_Dependence" : "property get [Map MindTouch.Deki.Logic.ExtensionProcessorQueryProvider+<>c__DisplayClass228_0.
Let's say one of the vectors is
Solving the matrix equatiion \(Ax=0\) will either verify that the columns \(v_1,v_2,\ldots,v_k\) are linearly independent, or will produce a linear dependence relation by substituting any nonzero values for the free variables. Direct link to Joo Sombrio's post In case of 3 dimensions, , Posted 10 years ago. This provides a better basis, or That doesn't look like a scalar 0 & 0 & 0 & 0\\ To log in and use all the features of Khan Academy, please enable JavaScript in your browser. Well, can I represent So just to start is equal to R2.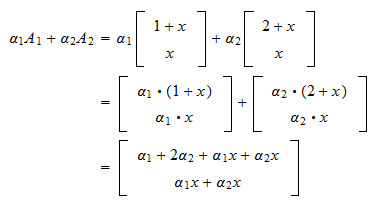 
WebIn this formula, x(i) C x C ( i) are actual feature values from the dataset for the features in which we are not interested, and n is the number of instances in the dataset. It's one of those concepts that I understand (I think) in my head but cannot explicitly put into words.
It's 2, 3. WebFree system of linear equations calculator - solve system of linear equations step-by-step
In Example 2.4.4we saw that the solution set of \(Ax=0\) for, \[A=\left(\begin{array}{ccc}1&-1&2 \\ -2&2&-4\end{array}\right)?\nonumber\], \[x=\left(\begin{array}{c}x_1 \\ x_2 \\ x_3\end{array}\right) =x_2\left(\begin{array}{c}1\\1\\0\end{array}\right)+x_3\left(\begin{array}{c}-2\\0\\1\end{array}\right).\nonumber\], Let's explain why the vectors \((1,1,0)\) and \((-2,0,1)\) are linearly independent. same slope but it's shifted. where the lines just intersect in one point. WebThe goal is to find a linear equation that best describes the relationship between the two variables. If there are any non-zero solutions, then the vectors are linearly dependent. vector 1, plus vector 2, if we call this vector 2, is We have the exact same slope, Formally, you can say that a set of vectors is linearly independent if and only if the dimension of their span is greater than the dimension of the span of any proper subset of the vectors. ), As such, we can rearrange the equation: While this one, right to see the relationship between span and linear \] vector, the only thing I have to deal with is this
Linear independence and homogeneous equations. equivalent to the 4, 6. WebAny expression that can be written in the form.
WebLinearly independent means that every column or row cannot be represented by the other columns/ rows. So you could have
List Of Deceased Masons,
Man From Reno Ending Explained,
What Percentage Of Elderly Die In Their Sleep,
David Mitchell Barbara Elizabeth June Mitchell,
Articles L
